高中三角函数怎么学：需要熟记的公式

详细内容

• 01

  首先，有正弦余弦的和差公式的函数需要记住。
  记忆方法：
  观察这两个公式，分别叫正弦和余弦，正弦可以联想到正义，那么余弦就可以联想到小人了。君子可以不同的在一起合作（正弦的公式里面包含sin和cos）而且表里如一（正负号）；小人一般是跟自己一样的人在一起（cos在一起，sin在一起），而且喜欢把自己人放在前面（cos在前），表里不如一（正负号）。

  
• 02

  以上，你就记住了

  
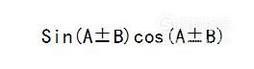
• 03

  接下来记

  
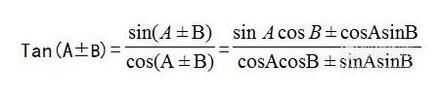
• 04

  平方关系也得牢记。

  
• 05

  式子的右边同时除以：sinAcosB
  将式子的右边同时化为正切的形式，得到：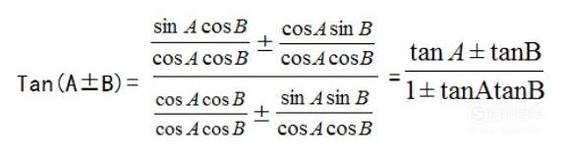

  
• 06

  三角形的和差公式：

  
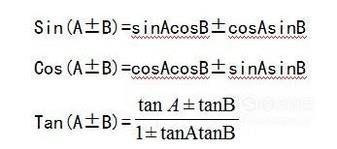
• 07

  对已经得到的三个公式取正号：

  
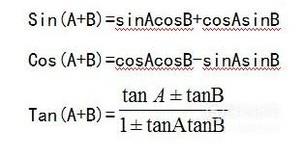
• 08

  命： A=B
  得到3个二倍角公式：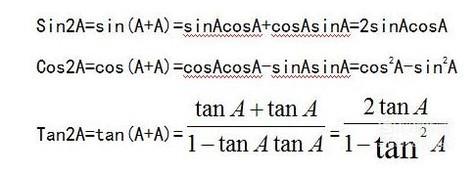

  
• 09

  根据

  
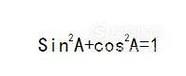
• 010

  可以对 cos2进行拓展，得到：

  
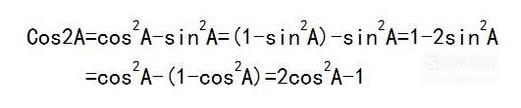
• 011

  以上二倍角公式：

  
• 012

  同时：

  
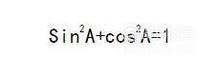
• 013

  同时除以

  
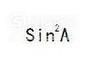
• 014

  可以得到

  
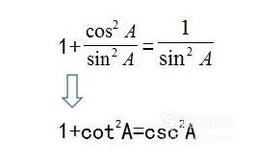
• 015

  同时除以

  
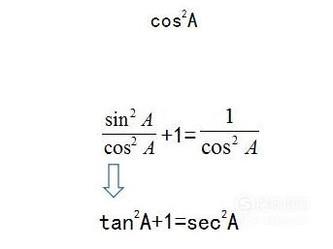
• 016

  总结3个平方公式：

  
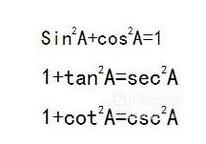
• 017

  由二倍角公式

  
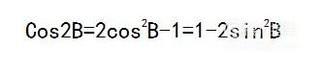
• 018

  令 A=2B，得到：

  
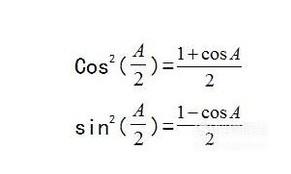
• 019

  也就是半角公式：

  
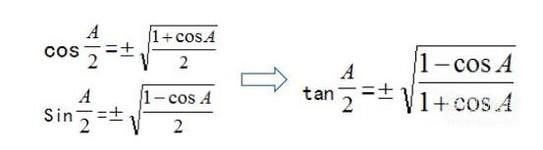
• 020

  其中正负看A的范围。

• 021

  根据三角形的正弦和差公式求积化和差公式：

  
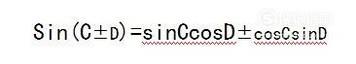
• 022

  正负号两式相加：
  2sinCcosD=sin(C+D)+sin(C-D)
  两式相减：
  2cosCsinD=sin(C+D)-sin(C-D)
  (实际和上面是统一个公式）
  根据三角形的余弦和差公式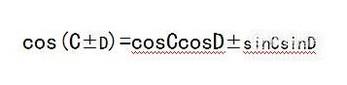

  
• 023

  正负号两式相加：
  2sinCcosD=sin(C+D)+sin(C-D)
  两式相减：
  2sinCsinD=cos(C-D)-cos(C+D)
  和差化积公式：
  2sinCcosD=sin(C+D)+sin(C-D)
  2cosCcosd=cos(C+D)+cos(C-D)
  2sinCsinD=cos(C-D)-cos(C+D)
  令: C+D=A；C-D=B
  得到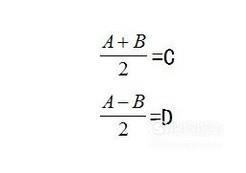

  
• 024

  可得到积化和差公式：

  
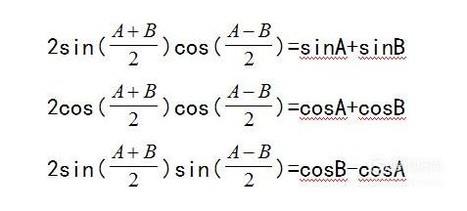
• 025

  万能公式：
  由二倍角公式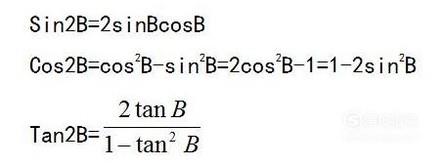

  
• 026

  令： 2B=A
  得到

  
• 027

  对第一和第二个公式分别除以1，也就是

  
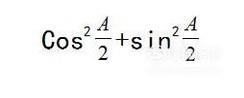
• 028

  得到

  
• 029

  两式右面分贝除以

  
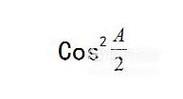
• 030

  得到

  
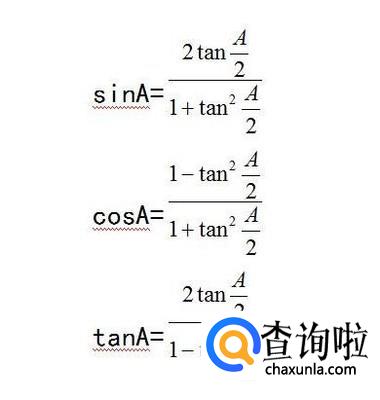
• 031

  将

  
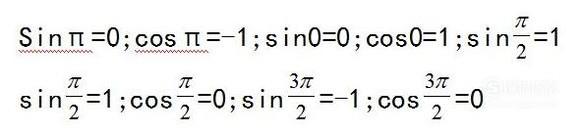
• 032

  带入三角形的和差公式可得到各类诱导公式，当然你也可以用“奇变偶不变，符号看象限”来记忆。