0.999999999循环等于1吗？

详细内容

• 01

  等于

  在数学的完备实数系中，循环小数0.999…表示一个等於1的实数，即0.999…所表示的数与1相同。目前该等式已经有各式各样的证明式；它们各有不同的严谨性、背景假设，且都蕴含实数的实质条件，即阿基米德公理、历史文脉、以及目标受众。

  

  无限循环小数 0.999... 与 1 严格相等。

  很多网友会通过一些初等的方法来理解这个事实，下面举出三种有代表性的初等思路：思路一：

  设 a=0.999...

  则 10a=9.999...

  于是 9a=10a-a=9.999...-0.999...=9,

  因此 a=1.

  思路二：

  由于 1/3=0.333...,

  所以 1=(1/3)×3=0.333...×3=0.999...

  

  思路三：

  0.999...可以看成首项为 0.9, 公比为 0.1 的等比数列

  

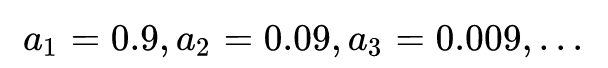
  的所有项之和.

  根据等比数列的求和公式,

  

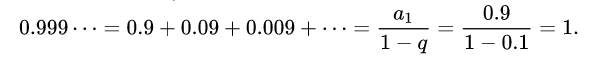
  但是，需要强调的是，以上三种思路可以用来直观理解，但不能把它们当成“1=0.999...”的严格证明。原因是，“0.999...”这样的无限小数的严格表示是超出了初等数学的范围的，不能想当然地对“0.999...”这样的无限小数做普通的加减乘除运算，所以上面三种初等思路只能算“投机取巧”的“初等理解”，而不能叫做“严格证明”。

  要给出 1=0.999... 这个事实的严格证明，需要理解从有理数构造实数的办法，这个构造过程将使我们更加深刻地认识无理数，而不是仅仅停留在"无限不循环小数"的直观层面上。

  

  在过去数十年裡，许多数学教育的研究人员研究了大众及学生们对该等式的接受程度，许多学生在学习开始时怀疑或拒绝该等式，而后许多学生被老师、教科书和如下章节的算术推论说服接受两者是相等的，尽管如此，许多人们仍常感到怀疑，而提出进一步的辩解，这经常是由于存在不少对数学实数错误的观念等的背后因素，例如认为每一个实数都有唯一的一个小数展开式，以及认為无限小（无穷小）不等于0，并且将0.999…视为一个不定值，即该值只是一直不断无限的微微扩张变大，因此与1的差永远是无限小而不是零，因此「永远都差一点」。我们可以构造出符合这些直观的数系，但是只能在用於初等数学或多数更高等数学中的标准实数系统之外进行，的确，某些设计含有「恰恰小於1」的数，不过，这些数一般与0.999…无关（因为与之相关的理论上和实践上都皆无实质用途），但在数学分析中引起了相当大的关注。