勾股定理公式怎么算？

详细内容

• 01

  在任何一个平面直角三角形中的两直角边的平方之和一定等于斜边的平方。在△ABC中，∠C=90°，则a²+b²=c²。勾股定理，是几何学中一颗光彩夺目的明珠，被称为“几何学的基石”，而且在高等数学和其他学科中也有着极为广泛的应用。

  

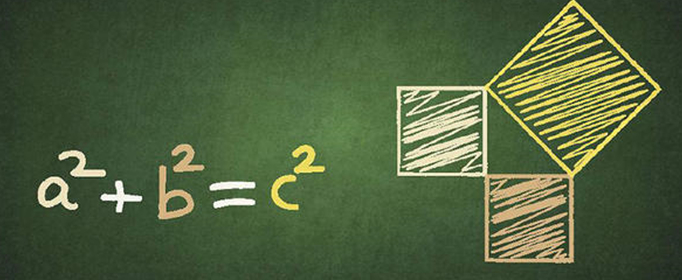
  勾股定理是一个基本的初等几何定理，直角三角形两直角边的平方和等于斜边的平方。如果直角三角形两直角边为a和b，斜边为c，那么a²+b²=c²，若a、b、c都是正整数，(a,b,c)叫做勾股数组。在任何一个平面直角三角形中的两直角边的平方之和一定等于斜边的平方。勾股定理，是几何学中一颗光彩夺目的明珠，被称为“几何学的基石”，而且在高等数学和其他学科中也有着极为广泛的应用。

  

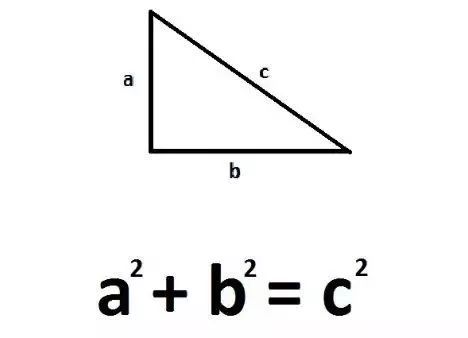
  勾股定理现约有500种证明方法，是数学定理中证明方法最多的定理之一。勾股定理是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。

  

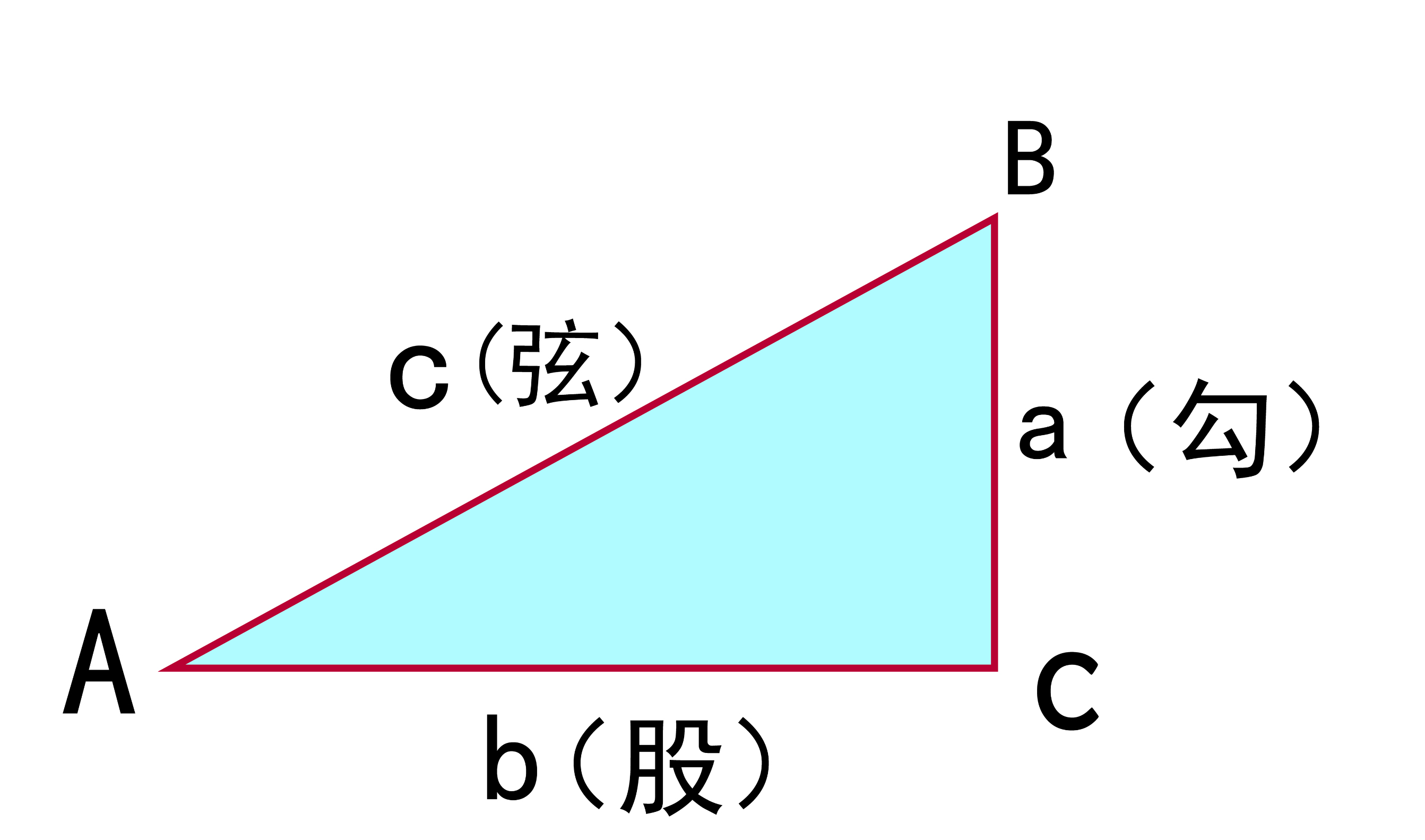
  在中国，周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。在西方，最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派，他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。